Mamba: Linear-Time Sequence Modeling with Selective State Spaces / Non-Attention 기반의 Sequence Model에 대한 접근

 

[논문]은 Mamba라는 이름의 Non-Attention 기반으로 순차적인 데이터를 추론하는 하나의 알고리듬이다.

Mamba: Linear-Time Sequence Modeling with Selective State Spaces

 

어쩌다 이런 알고리듬까지 등장하게 되었을까?

간단하게 역사를 살펴보자.

Attention is all you need

 

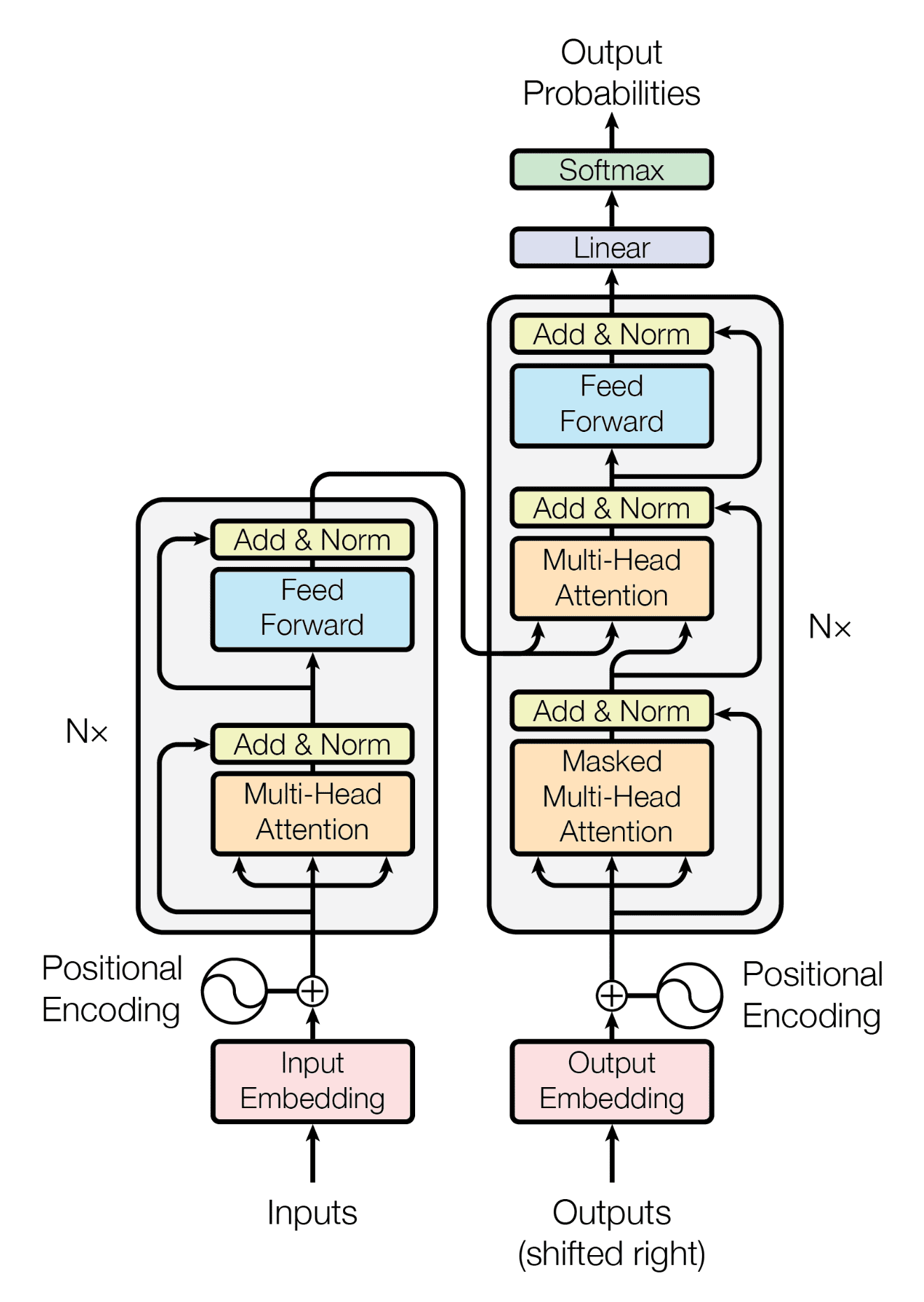
최근 유망한 LLM의 기반은 모두 Google의 Transformer로 부터 출발하였다 보아도 과언이 아니다.

Transformer는 사뭇 대단해보이지만, 까고 보면 결국 다음 단어의 Embedding을 예측하는 하나의 예측 모델일 뿐이다.

 

즉, 이전 상태의 Embedding 을 보고 다음 상태의 Embedding을 맞추는 하나의 Next Sequence Prediction을 수행하고
이 과정에서 이전 상태의 임베딩들의 관계를 고려할 수 있는 'Attention'을 통해 성능을 끌어 올린다.

 

그런데 왜 Attention이 필요하게 되었을까?

이전 상태를 고려하는 알고리듬은 예전부터 존재했다.

Recurrent Neural Network(RNN)

 

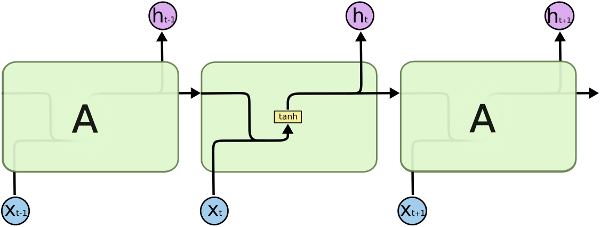
RNN은 이러한 시도의 가장 기본적인 형태라고 볼 수 있다.

현재 상태의 예측값을 고려하기 위해서, 이전 상태의 결과를 함께 사용하는 것이다.

RNN은 위와같은 아주 간단한 방법으로 시간적인 특성을 반영하는 데 성공한 것이다.

 

문제는 순차적이라는 특성에 의해 몇 가지 문제가 발생하는데,

가장 대표적인 문제는 Long-Sequence에 제대로 대처하지 못하는 것이다.

 

형태에서 알 수 있듯이, 이전 상태의 출력을 다음 상태의 입력과 함께 사용하는 구조로 길이가 길어진다면

앞선 정보가 효과적으로 마지막 상태까지 전달되지 못하는 것이다.

Long Short-Term Memory (LSTM)

 

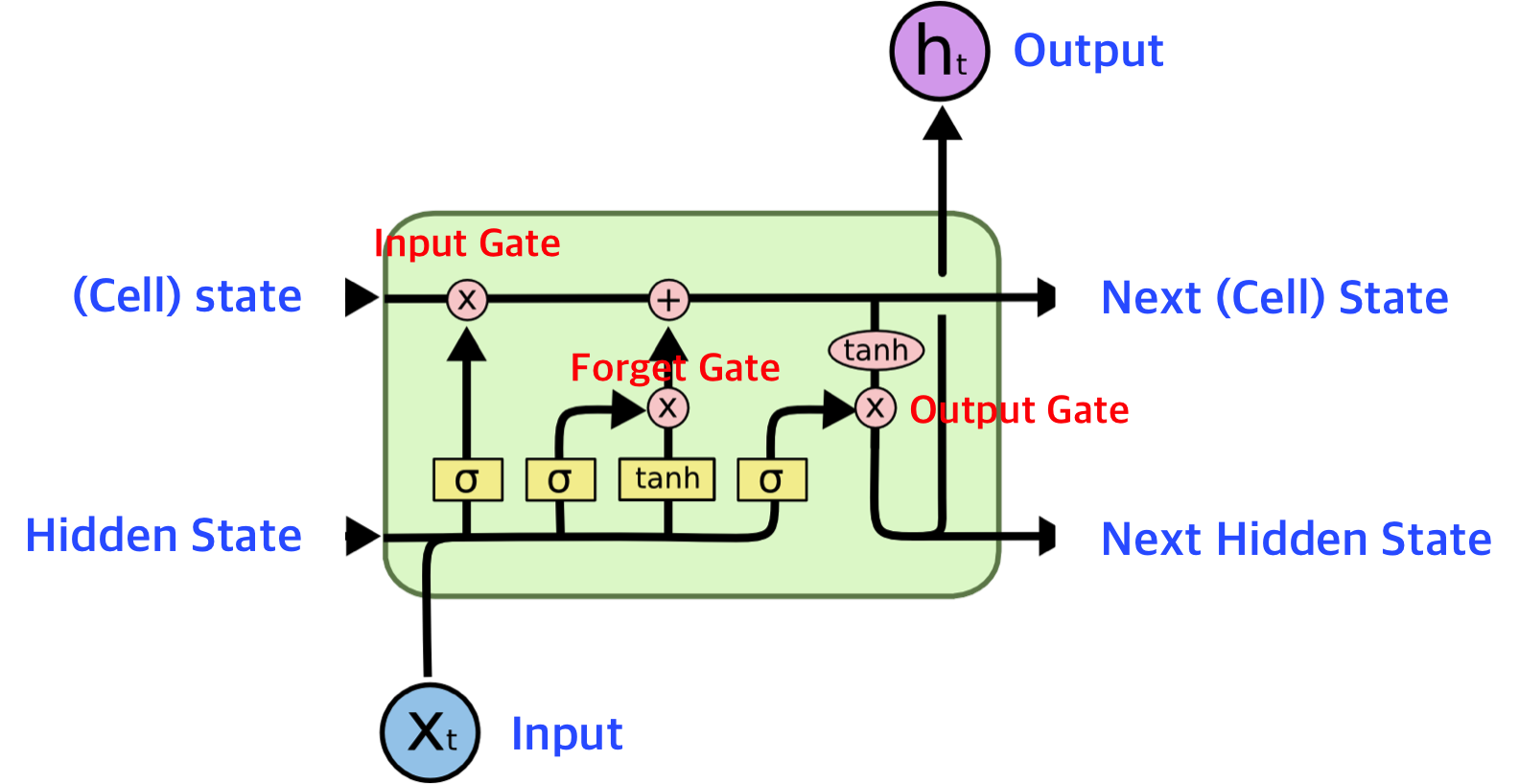
이런 문제를 직접적으로 해결하기 위해 LSTM이 등장한다.

아주 간단하게 이해하면, RNN에서 사용하던 메커니즘은 그대로 유지한 체

무엇을 다음 상태로 넘겨줄지 결정하는 하나의 Cell Container가 추가된 모습이다.

 

LSTM은 상당히 효과적인 알고리듬으로 실제로 당시 존재하는 많은 Sequence 문제를 해결하는 것처럼 보였다.

그러나 이러한 Sequence 모델이 가지고 있는 근본적인 한계가 존재하였는데

 

그건바로 현재 X_t 의 상태를 추론하기 위해서는 반드시 X_t-1의 상태에 대한 결과를 가지고 있어야 한다는 것이다.

 

결국 Long-Sequence를 효과적으로 대처하는 능력자체는 가지고 있으나 ...

이를 위해서는 순차적으로 모든 상태를 계산하고, 이것을 다음 상태로 넘겨주는 작업을 모두 계산해야 한다는 것이다.

그것도 모든 단일 Sequence를 마주하는 모든 순간에 말이다 ...

이러한 문제는 결국 Memory가 절대로 병렬화 될 수 없음을 의미하며
Sequence가 커지면 커질수록 ... 모델이 커지면 커질수록 학습의 속도가 매우매우 느려진다 ..

 

이러한 역사의 흐름 속 2015년 Attention Mechanism이 등장하게 된다 [링크]

Neural Machine Translation by Jointly Learning to Align and Translate

그리고 순차적으로 2017년 Google의 Transformer가 등장하며 Sequence 데이터 처리의 문제를 해결하게 된다.

Wang, J., Li, M., Diao, Q., Lin, H., Yang, Z., & Zhang, Y. (2020). Biomedical document triage using a hierarchical attention-based capsule network. BMC bioinformatics, 21, 1-20.

 

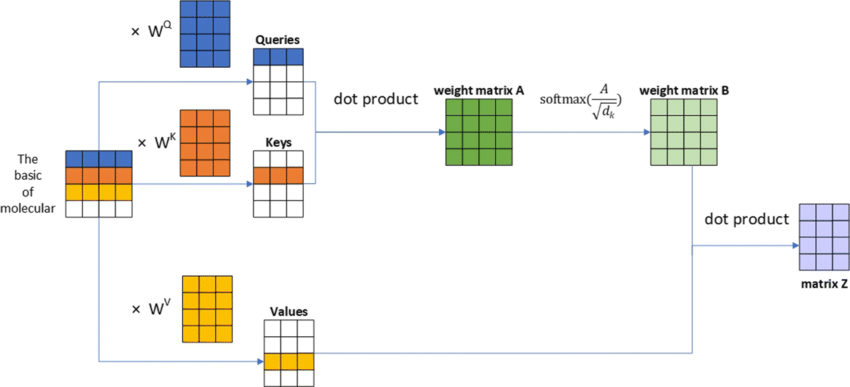
이를 해결하는 핵심이 바로 Attention Mechanism의 핵심인 Key, Query, Value Matrix라고 볼 수 있다.

Transformer에서 학습하게되는 파라미터는 바로 이 세가지 행렬에 담겨있는데,

Input으로 들어오는 Embedding된 벡터와의 행렬연산을 통해 상당히 빠른 속도로 추론이 가능하다는 장점이 있다.

 

이러한 행렬 연산에 의해 이전 정보와의 관계성 (여기서는 Attention Score)을 표현하기 때문에

앞선 RNN 기반 알고리듬의 문제 중 하나였던 t-1의 상태를 계산할 필요가 없다는 것이다.

 

즉, 시간적 혹은 순차적인 관계성을 표현하는 데 있어서 Sequencial한 추론 과정이 배제될 수 있다는 것이다!

이러한 특성 때문에 해당 Weight Matrix는 병렬적인 학습이 가능했으며
Long-Sequence를 다루는 것에 있어서도 상당히 강력한 성능을 보였고
기본적으로 행렬연산을 수행하기 때문에, Parameter의 숫자에 비해 상당히 빠르다

 

이러한 기능 때문에 Transformer 이후의 모델들은

더 큰 모델로 .. 더 많은 파라미터로 .. 더 많은 Attention head를 이용하며

이를 대처하기 위해 상당히 많은 GPU를 사용하여 문제를 해결하였다.

Wei, J., Tay, Y., Bommasani, R., Raffel, C., Zoph, B., Borgeaud, S., ... & Fedus, W. (2022). Emergent abilities of large language models. arXiv preprint arXiv:2206.07682.

 

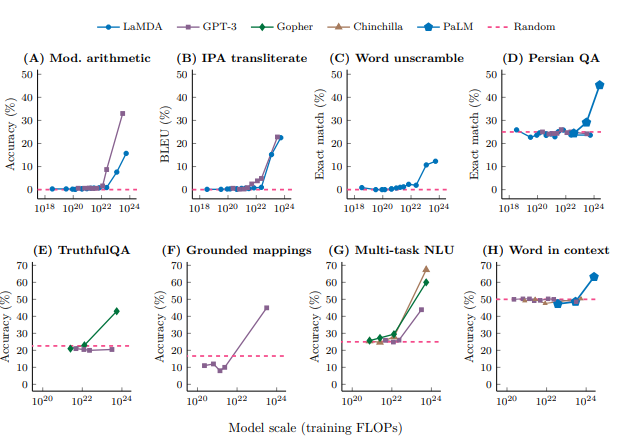
이러한 와중 이러한 Bigger is Better 풍조에 기름을 부어버리는 사건이 발생한다.

2022년 (또 다시 Google)에서 발표한 논문에 따르면 10^22의 파라미터를 뛰어넘는 단계에서

갑작스러운 성능의 향상이 나타난다는 논문이 발표된다.

 

창발적 능력(Emergence Ability)라고 부르는 이 현상은 Next-Word-Predict 모델의 크기가 커짐에 따라

우리가 기대하였던 ... 말 그대로 다음 단어를 추론하는 것을 뛰어 넘어 어떠한 알 수 없는 능력을 갖게 된다는 것이다.

Unsupervised sentiment neuron [https://openai.com/index/unsupervised-sentiment-neuron/]

 

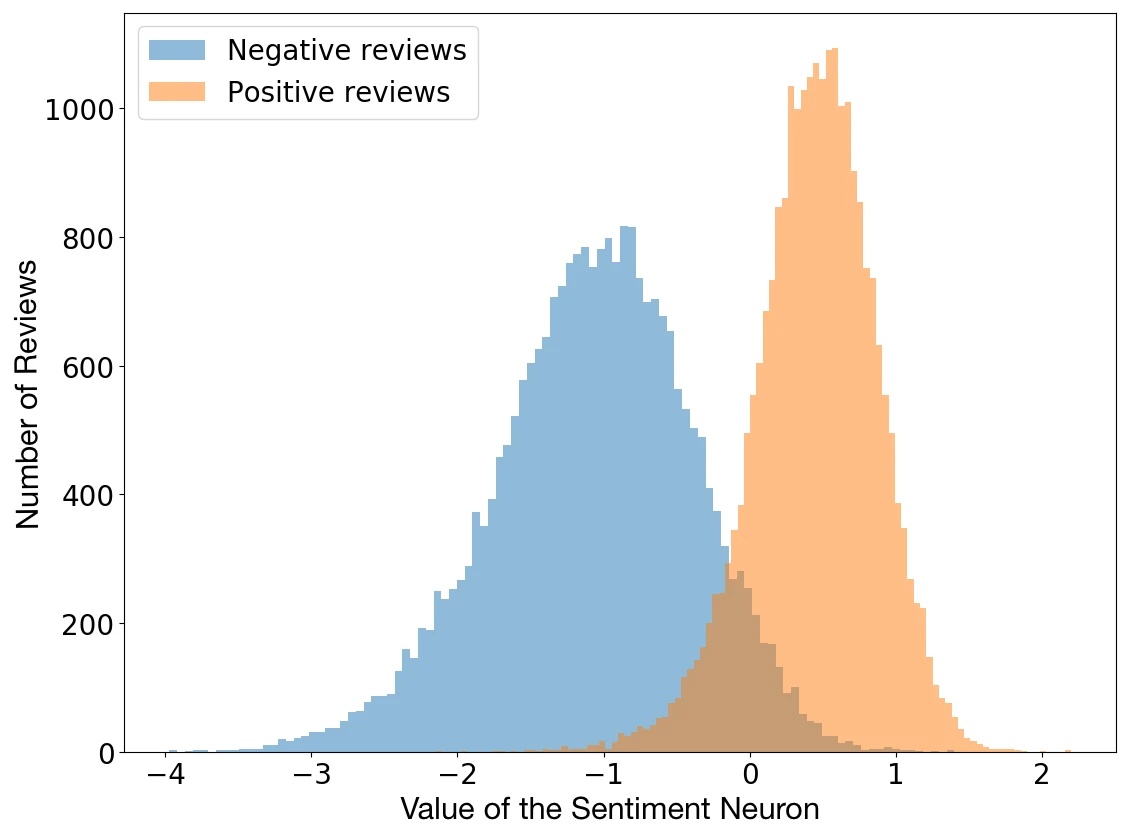
이는 2017년 OpenAI의 Blog에서도 확인할 수 있는데

Sentiment Analysis와는 전혀 다른 Task를 수행하던 모델임에도 불구하고

어떠한 Neuron의 결과는 Sentiment Analysis의 결과의 형태를 띄고 있었다는 것이다.

 

이후 Transformer는 Sequence한 문제 영역에서 강력한 헤게모니를 차지하게 되었다만 ...

Transformer에는 문제가 없었을까?

 

꼭 그렇지는 않다.

모든 Token의 관계를 (정확하게는 Embedding된 Vector) 표현하고 있던 Parameter들은 매우 무거운 도구가 되어버린다.

 

즉, '사람'이라는 단어와 '동물'이라는 단어의 Attention Score를 계산하기 위해서 Transformer는 모든 Parameter를 가져와야 한다 ...

 

즉 아주 간단한 작업일지라도, 엄청난 Cost를 사용하게 된다는 것이다.

더불어 크기가 커지면 거질 수록, 이러한 엄청난 녀석을 GPU에 Load하는 것부터 문제가 생겨버린다.

 

즉 학습에서 좋았던 녀석이 Inference에서는 심각한 단점을 야기한다는 것이다.

이러한 역사 속에서 Non-Attention을 이용한 Space-State Model 기반 연구들이 등장하기 시작한다.

---

Recurrent Neural Network(RNN)

 

무엇을 기억할지(전달할지) 기억하기 vs 기억을 복원하는 방법(규칙)을 기억하기

 

RNN Parameter가 학습하고 있는 것은

"과거의 시점에 발생한 기억들을 어떻게 현재로 가져올 것인가?"에 대한 부분이다.

 

계속 언급하지만 RNN은 특정 Sequence 전체를 살펴보며 비구조화된 순차적인 정보전달의 메커니즘을 가진다.

즉 현재상태 (t)에서 이전상태(t-1)의 정보를 얻어내기 위해, Sequence의 첫 상태(t_0)까지 가야하는 문제가 생긴다.

 

앞서 보았듯 이를 해결하기 위해 Transformer는 전체 Sequence에 대한 Attention 정보를 통해
Long Sequence의 문제를 효과적으로 대처한다. 그러나 이건 매우 크고 무겁다는 단점이 존재한다.

 

기억을 끄집어내는 방식을 기억할 수 있는 형태로 규정할 수 있다면

t-1의 상태가 필요하다면, 적절한 규칙에 의해 t-1을 얻을 수 있기만 하면 되는 것이 아닌가?

Gu, A., Goel, K., & Ré, C. (2021). Efficiently modeling long sequences with structured state spaces.  arXiv preprint arXiv:2111.00396 .

 

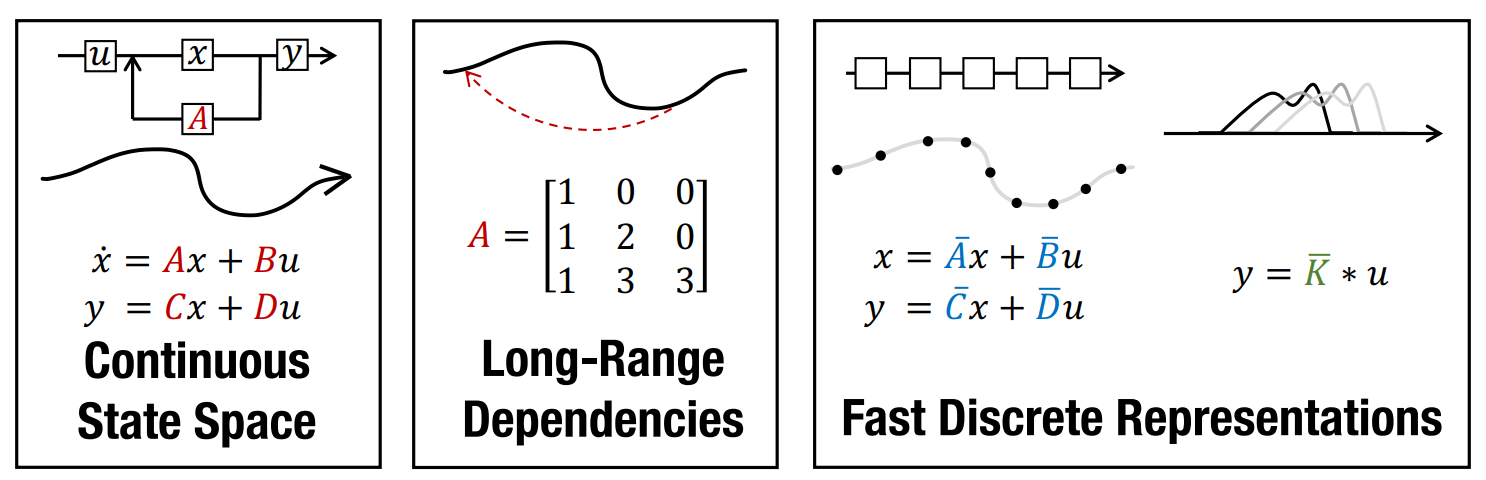
이러한 문제를 해결하기 위해 새로운 접근 방식들이 시도 된다.

State Space Model은 제어 이론이나, Computational Neuroscience 등 다양한 분야에서는 이미 널리 효과가 입증된 모델이지만, 우리가 다루고자 하는 Long-Sequence의 Deep Learning영역에서는 두각을 보이고 있지 않았다.

 

이러한 SSM의 핵심적인 아이디어는 우리가 찾고자하는 어떠한 State x가 이산화된 동일한 미분 방정식으로 표현되며

이러한 미분 방정식의 핵심 요소인 matrix A가 모든 Linear Time-Invariant한 특징을 지닌다는 것이다.

 

즉, Sequence를 구성하는 모든 State가 하나의 Linear System에 의해서 표현될 수 있다는 것이다.

이렇듯 명백하게 구조화된 형태로 Sequence의 State가 표현되는 것이 SSM의 핵심적인 가치라고 볼 수 있다.

떄문에 전통적 모델에서 핵심 구성요소인 matrix A는 기본적으로 해당 Model 내부에서 동일한 값을 가진다.

그러나 이러한 빙식의 모델링은 고차원 비선형적 특징을 띄는 State를 적절하게 매핑하지 못하는 문제가 발생한다.

다시 RNN

 

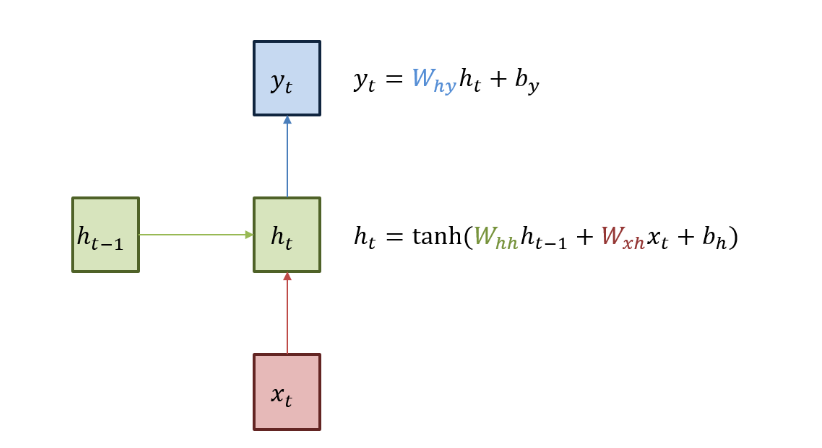
그러면 matrix A가 time t에 따라 변동적인 값을 가지면 되는 것이 아닌가?

그러나 변동적 특징과 함께, 학습가능한 형태를 띄면 그것이 결국 RNN과 다를 바가 없어지며 (특징은 거의 유사하다)

결국 달성하고자 했던 구조화된 수식을 통해 전체 State의 latent space를 구축하는 것이 어려워진다.

 

HiPPO는 이러한 문제를 구조화 행렬을 통해 효과적으로 해결할 수 있음을 입증한다.

 

즉 전통적 방식에서의 Matrix A가 "고정 행렬"이며
RNN과 같은 자유로운 상태의 Deep Learning Method에서는 "비구조화된 행렬"이라면

 

HiPPO는 "구조화 행렬"을 통해 Matrix A를 구성하고,

이를 통해 효과적으로 Sequence의 State를 표현할 수 있음을 보여주고 있다.

 

Gu, A., Dao, T., Ermon, S., Rudra, A., & Ré, C. (2020). Hippo: Recurrent memory with optimal polynomial projections.  Advances in neural information processing systems ,  33 , 1474-1487.

 

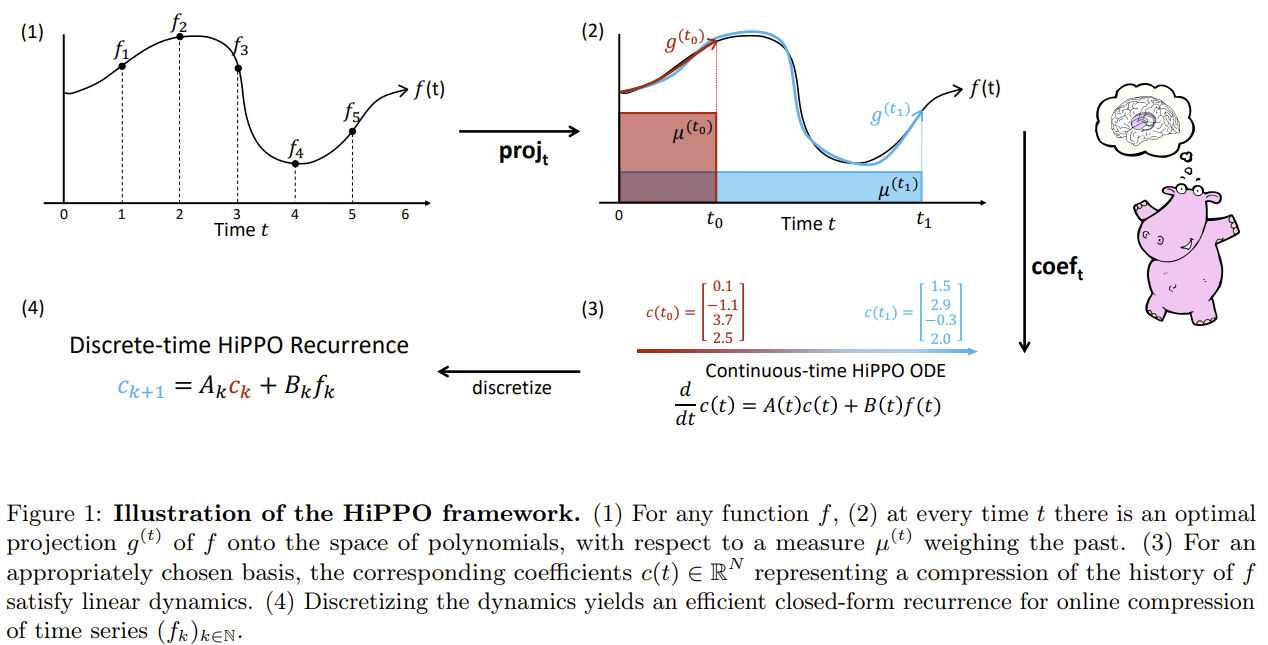
우리는 앞서 이야기 했듯, 어떠한 상태를 Time-Invariant한 이산적인 미분 방정식으로 표현하고 싶다.

그러면서 원본 상태를 효과적으로 묘사할 수 있으면서도

이를 위해 필요한 Matrix A가 상당히 구조화된 방식을 띄고 있으면 좋겠다는 것이다.

 

이것이 바로 Mamba라는 지식 구조의 블럭 중 하나인 HiPPO라고 볼 수 있다.

HiPPO는 그림에서 알 수 있듯이 [프로젝션] -> [계수추정] -> [이산화] 세 가지로 이뤄진 기억의 저장법이라고 볼 수 있다.

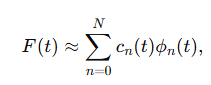
프로젝션과 계수추정이 이뤄지면, 모든 Time T에 대해 위와 같은 근사가 성립된다.

여기서 파이(T)는 Orthogonal Polynomial Basis를 의미하며 (르장드르 다항식만 살펴보자)

이러한 직교 다항식과 계수를 통해서 원본 상태를 근사할 수 있음을 보이고 있다.

 

어차피 Orthogonal Polynomial Basis는 고정된 상태를 띄고 있기 때문에

복원을 위해 실질적으로 기억하는 정보는 계수함수 c(T)로 볼 수 있는데

 

(매우 복잡한 수식과 함께 ...) HiPPO에서는 이 또한 이산화된 미분 방정식을 통해 계산해 두었다.

 

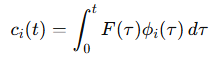
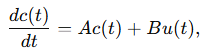
실제 c(T)를 적분하여 구하는 것은 매우 어려우니 ...

c(T)의 변화량을 A와 B라는 어떠한 Matrix와의 미분 방정식으로 표현이 가능하다.

 

(또 매우 복잡한 수식과 함께 ...) 이러한 미분 방정식은 이산적인 상태 방정식으로 표현이 가능하고

우리가 원본함수 F를 추정하기 위해 필요한 모든 정보 C는, 매우 구조화된 Matrix A와 연속적인 상태로 구할 수 있다.

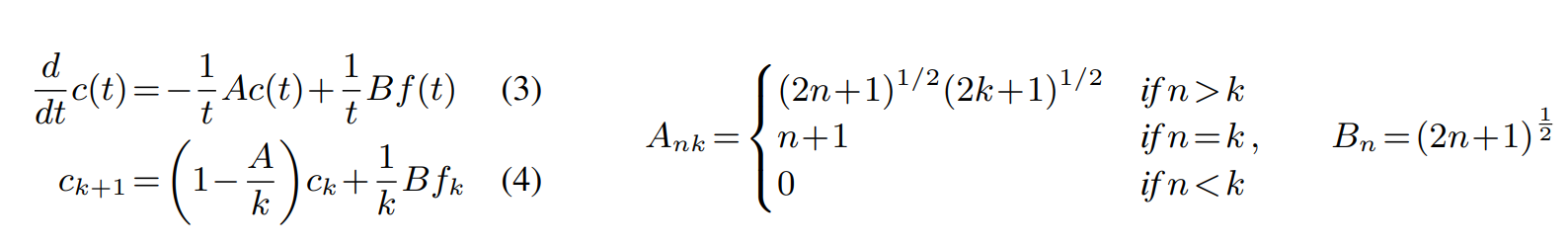
즉 상기 목표하였던 S_t+1 = Matirx A * S_t 의 형태를 LTI System 내부에서 모두 유지하면서, 구조화된 Matrix A를 통해
효과적으로 Long-Sequence를 처리할 수 있음을 증명하고 있다.

---

여기까지 SSM 겉핥기를 진행해 보았다.

 

한 줄로 요약하여 생각해본다면

RNN과 같은 모델이 학습을 통해 가지고 있는 Hidden State를 구성하는 Function을

Linear Time-Invarient한 시스템 상에서 상태방정식을 통해서 표현하는 방법론이라고 보면 되겠다.

 

뒤에서는 HiPPO와 S4를 더 자세하게 살펴보겠다.