Topic. 딥러닝을 이해하기 위해 필요한 수학적 지식을 설명합니다.
AI 와 수학
쉽게 설명하자면 AI는 확률적 통계를 이용한 프로그램에 가깝습니다. 통계는 숫자를 이용하여 나타납니다.
기존 데이터가 수치로 표현되어 있다면 해당 수치들을 이용하여 딥러닝을 할 수 있습니다.
LLM 과 같이 챗봇으로 사용되는 생성형 AI 모델을 이용할 때에는 문자를 컴퓨터가 이해할 수 있도록 숫자로 표현해야 합니다.
이렇게 일상생활에 일어나는 상황들을 숫자로 변환하는 작업을 임베딩(embedding) 이라고 합니다.
임베딩의 결과로 나타난 숫자들은 배열로 표시됩니다.
예를들어 알파벳 a 부터 z 까지 1-26 까지 숫자를 붙인다고 가정했을 때 'apple' 은 [1,16,16,12,5] 로 임베딩됩니다. 이렇게 숫자로 변환한 후 요런 저런 함수를 이용하여 학습을 시키는 작업을 진행하게 됩니다.
상황을 수학과 연결시켜보기

이 좌표는 공부시간에 따른 시험성적을 표시할 수 있는 좌표입니다. 이 좌표에 각 학생의 성적을 점으로 찍어보겠습니다.

X축은 공부시간이고 Y축은 성적입니다. 따라서 이좌표는 공부시간에 따른 성적좌표입니다. 빨간색 점은 각 학생이 공부한 시간에 따른 성적을 나타냅니다. 이 좌표에 찍힌 빨간점들을 보고 점이 찍히지 않은 X축 중 65시간과 75시간에 대한 성적을 예측을 하고자 합니다.
일차 함수, 기울기와 y 절편

일차함수로 예측을 시도해 보려고 할 때 대충 선을 그어보았습니다. 대충 그어보았기에 정확한 예측선은 아닙니다. 이제 이 선을 각각 학생의 점수를 반영하여 조정해 보려고 합니다. 직선을 조정하려면 직선의 기울기와 Y축과 만나는 시작지점만 정해지면 수정이 가능합니다.여기서 기울기를 a 라 하고 y축과 만나는 지점(Y절편) 을 b 라고 할 때 직선 그래프는 y=ax+b (a != 0, b >=0) 로 나타낼 수 있습니다.
우리의 목표는 x가 주어지고 원하는 y값이 있을 때 적절한 기울기 a와 y절편 b를 구하는 것입니다.

일차함수 그래프에서의 기을기는 y증가량 나누기 x증가량 입니다.
이차 함수와 최솟값
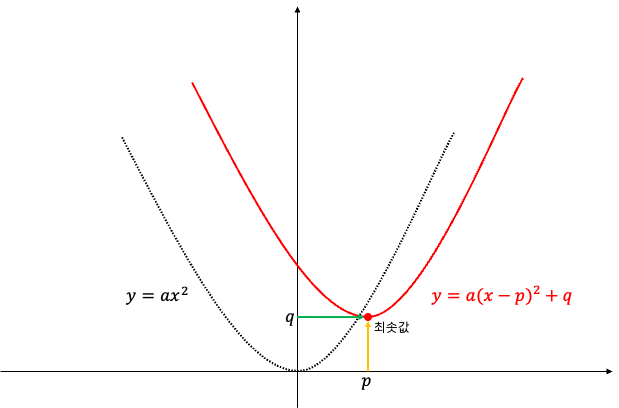
이번에는 이차함수를 살펴보겠습니다. 위 일차함수에서 기울기 a와 y절편 b를 구하기 위해서는 이차함수가 필요합니다.
y=ax^2 그래프를 x축 방향으로 p만큼, y축 방향으로 q만큼 이동시킨 그래프는 y=a(x-p)^2 + q 입니다.
그림에서 빨간점은 이 이차함수 그래프의 최솟값입니다. 딥러닝을 실행할 때 이 최솟값을 찾는것이 매우 중요합니다. 이 최솟값을 찾기 위해서는 미분과 기울기를 이용해야합니다. 이 최솟값을 찾아야 하는 이유를 알기 위해 미분과 기울기의 관계를 먼저 알아봅시다.
미분과 기울기
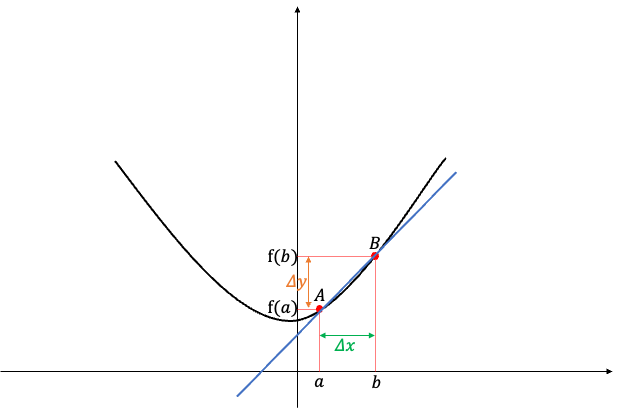
이차함수 그래프 위의 점 A, 점 B 가 있다고 가정했을 때 A와 B를 이은 직선의 기울기를 구해봅시다.
여기서 x는 이차함수를 따라 움직입니다. 이에 따라 y도 x가 이차함수를 따라 움직이는 것처럼 움직입니다.
따라서 x와 y는 Δ(델타)를 이용하여 변화하는 값으로 Δx, Δy 라고 표기합니다.
이 그래프에서
x값의 증가량 Δx 는 f(b)-f(a) 입니다.
y값의 증가량 Δy 는 b-a 입니다.
이때 b = a + Δx 입니다.
직선 AB의 기울기
= y증가량 나누기 x증가량
= Δy / Δx
= ( f(b)-f(a) ) / ( b - a )
= ( f(a + Δx)-f(a) ) / ( a + Δx - a )
= ( f(a + Δx)-f(a) ) / Δx
순간변화율은 a와 b 사이의 거리 즉 Δx 가 0에 아주 가까울 정도로 작을 때의 기울기를 의미합니다.
결론적으로 순간변화율 공식은 아래와 같습니다.
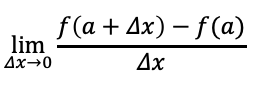
미분을 한다는 것은 바로 이 순간변화율을 구하는 것이며, 원래 점과 아주 작게 이동한 x의 점을 이어 직선으로 만들면 접선이됩니다.
이 접선의 기울기를 구하는 것이 바로 미분입니다.
결론적으로 미분이 필요한 이유는
y = ax + b 에서 a는 기울기라고 했습니다.
a가 무한정 커지거나 무한적 작아진다면 직선의 기울기는 어떻게 될까요?
위 그래프와 같이 y축과 점점 일치하게 될것입니다.
즉, a가 무한정 커지면 오차가 커질것이고 반대로 무한정 작아져도 오차가 커지기에 이 모습에서
x축을 기울기로두고
y축을 오차로 두면
아래와 같이 y=x^2 과 같은 이차함수 모양이 나타날 것입니다.
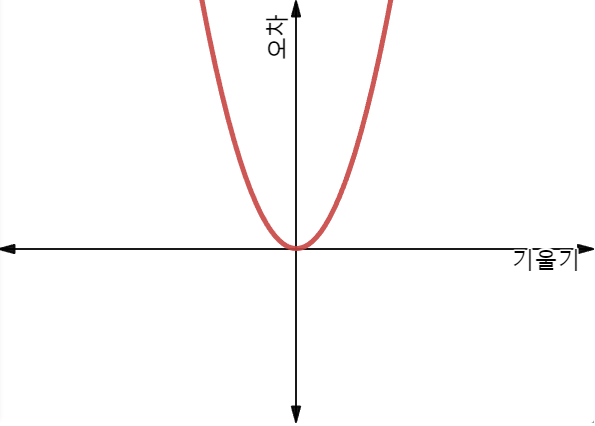
따라서 우리는 오차가 가장 작은 기울기가 0이 되는 지점을 찾기 위하여
미분을 사용한다고 보시면 되겠습니다.
'A.I.(인공지능) & M.L.(머신러닝) > A.I. Information' 카테고리의 다른 글
| [이론] 퍼셉트론 이란? (0) | 2024.01.16 |
|---|---|
| [이론] LoRA (Low-Rank Adaptation) (0) | 2024.01.11 |
| [수학] 가우스함수 (2) | 2023.12.07 |
| 3. 선형 회귀 모델 & 경사하강법 (1) | 2023.11.01 |
| 1. 인공지능? 머신러닝? 딥러닝? (0) | 2023.10.12 |





