2. 초간단 신경망(2/3)

이전 장에서는 경사하강법, 활성화 함수, 오차함수에 대해서 알아봤다. 이번 장에는 이전 장에서 구성된 파이썬 소스를 이용해 가장 단순한 형태의 신경망을 구성해본다. 신경망 네트워크는 2계층을 구성한다.

network.py

from layers import *
from gradient import *


class TwoLayerNet:
    # 생성자에서 하이퍼 파라미터를 받는다
    def __init__(self, input_size, hidden_size, output_size, weight_init_std=0.01):
        # 가중치(Weight) 초기화
        # W1, W2 가중치는 정규 분포로 초기화
        # b1, b2 편향은 0으로 초기화
        self.params = {
            'W1': weight_init_std * np.random.randn(input_size, hidden_size),
            'b1': np.zeros(hidden_size),
            'W2': weight_init_std * np.random.randn(hidden_size, output_size),
            'b2': np.zeros(output_size)
        }

    # 예측, 추론
    def predict(self, x):
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.matmul(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.matmul(z1, W2) + b2
        y = softmax(a2)

        return y

    # 손실함수
    def loss(self, x, label):
        y = self.predict(x)

        return cross_entropy_error(y, label)

    # 정확도 계산
    def accuracy(self, x, label):
        y = self.predict(x)
        y = np.argmax(y, axis=1)

        # if label.size == y.size:
        #     label = np.argmax(label, axis=1)

        accuracy = np.sum(y == label) / float(x.shape[0])
        return accuracy

    # 가중치 매개변수의 기울기를 구한다.
    def numerical_gradient(self, x, label):
        def loss_weight(W):
            return self.loss(x, label)

        grads = {
            'W1': numerical_gradient(loss_weight, self.params['W1']),
            'b1': numerical_gradient(loss_weight, self.params['b1']),
            'W2': numerical_gradient(loss_weight, self.params['W2']),
            'b2': numerical_gradient(loss_weight, self.params['b2'])
        }

        return grads

MNIST 데이터셋

pip install mnist

MNIST 데이터베이스는 http://yann.lecun.com/exdb/mnist/ 에서 사용할 수 있다

MNIST 데이터베이스는 손으로 쓴 숫자의 데이터셋인데 여기에는 60,000개의 훈련 샘플과 10,000개의 테스트 샘플이 있다. 각 이미지는 28x28 픽셀로 표시되며 각 이미지에는 회색조 값과 함께 0 - 255 값이 포함되어 있다.

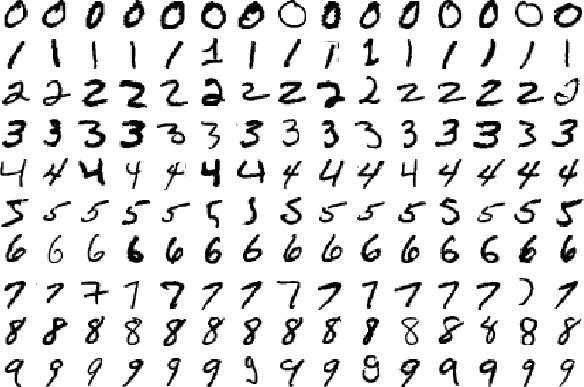
숫자의 크기 정규화되었으며 고정 크기 이미지의 중앙에 배치되어 있다. 전처리 및 포맷팅에 최소한의 노력을 들이면서 실제 데이터에 대한 학습 기술 및 패턴 인식 방법을 시도하려는 사람들에게 좋은 데이터베이스이다.

학습 및 테스트, 이미지 및 레이블이 별도로 포함된 4개의 파일을 사용할 수 있다.

자동으로 다운로드하고 데이터 세트의 첫 번째 이미지를 표시하려면 아래오 같이 한다.

import mnist
from matplotlib import pyplot as plt

images = mnist.train_images()
plt.imshow(train_images[0, :, :] * -1 + 256, interpolation='nearest')

테스트 파일과 라벨은 비슷한 방법으로 다운로드할 수 있다. 한번 다운로드 받으면 캐시되어 다시 다운되지 않는다.

import mnist

train_images = mnist.train_images()
train_labels = mnist.train_labels()

test_images = mnist.test_images()
test_labels = mnist.test_labels()

숫자 하나의 이미지는 2차원 행렬(2D)로 표현할 수 있다. 전체 데이터셋은 3D numpy 배열(샘플인덱스 * 행 * 열)로 반환되는데, 여기에서는 2D 배열로 변환된다(샘플인덱스 * 1차원으로 변환된 이미지)

이렇게 변환하기 위해서는 아래와 같이 수행한다.

import mnist

train_images = mnist.train_images()
x = trains_images.reshape((images.shape[0], images.shape[1] * images.shape[2]))

네트워크(TwoLayerNet 신경망) 활용

이제 신경망을 네트워크를 구동하는 기능을 만들어 보자. 잘 알려진 딥러닝 프레임워크인 Pytorch, Tensorflow 등을 이용할 때는 개발자는 프레임워크에서 제공되는 네크워크의 레이어 기능을 '활용' 하여 '네크워크를 구성하는' 기능을 주로 만들게 된다. 우선 아래와 같이 코드를 작성하자.

import mnist
from matplotlib import pyplot as plt

from network import *

# 학습용 이미지
train_images = mnist.train_images()

# 학습전에 실제 이미지를 확인해 보자.
# plt.imshow(train_images[0, :, :] * -1 + 256, interpolation='nearest')
# plt.show()
train_x = train_images.reshape(train_images.shape[0], train_images.shape[1] * train_images.shape[2]) / 255
train_labels = mnist.train_labels()

# 검증용 이미지
test_images = mnist.test_images()
test_x = test_images.reshape(test_images.shape[0], test_images.shape[1] * test_images.shape[2]) / 255
test_labels = mnist.test_labels()

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

# 손실율 저장
train_loss_list = []
train_acc_list = []
test_acc_list = []

# 하이퍼 파라미터
iters_num = 10000
train_size = train_x.shape[0]
batch_size = 100
learning_rate = 0.1

# 1 epoch 당 반복 수
iter_per_epoch = max(train_size / batch_size, 1)

for i in range(iters_num):
    # 미니배치 획득
    batch_mask = np.random.choice(train_size, batch_size)
    batch_x = train_x[batch_mask]
    batch_labels = train_labels[batch_mask]

    # 기울기 계산
    grad = network.numerical_gradient(batch_x, batch_labels)

    # 매개변수 갱신
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 학습 경과 기록
    loss = network.loss(batch_x, batch_labels)
    train_loss_list.append(loss)

    # 1에폭당 정확도 계산
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(train_x, train_labels)
        test_acc = network.accuracy(test_x, test_labels)
        train_acc_list.append(train_acc)
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

# 정확도 그래프 그리기
markers = {'train': 'o', 'test': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, test_acc_list, label='test acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

이렇게 네트워크를 구성해서 활용하는 경우에 주로 하는 작업의 순서는 아래와 같다.

데이터셋을 불러온다.
데이터셋에 대해 정규화 등의 전처리 작업을 한다.
데이터셋을 학습 데이터와 검증 데이터로 분리한다.
네트워크의 모양(층의 길이, 활성화 함수의 종류)을 결정하여 네크워크 모델을 구성한다.
반복횟수, 미니배치의 크기, 학습률, 학습량 등의 하이퍼 파라미터를 결정한다.
결정된 하이퍼 파라미터에 따라 학습을 반복하며, 손실율, 정확도 등을 계산하여 저장된다. 통상 1 epoch 이 수행될 때 화면에 학습 로그를 출력한다.
6번의 손실율, 정확도를 로그파일로 남기고, 차트로 시각화 한다.

위 소스에서는 정확도를 그래프로 그리고 있는데, 손실율도 저장하고 있으니, 같은 방법으로 손실율 그래프도 그려보길 바란다. 정확도 로그는 아래와 비슷한 숫자로 출력될 것이다. 그런데 GPU를 활용하지도 않고, 수식 연산되도 최적화 되어 있지 않은 소스이기 때문에 상당한 시간이 걸린다. 나 같은 경우는 CPU 가 라데온 5950 인데도 50시간 정도가 걸렸다.

성능을 최적화 하기 위해서는 수식연산인 기울기(미분) 연산을 개선해야 한다.

train acc, test acc | 0.09751666666666667, 0.0974
train acc, test acc | 0.76545, 0.7704
train acc, test acc | 0.8198833333333333, 0.8233
train acc, test acc | 0.8263833333333334, 0.8292
train acc, test acc | 0.8362666666666667, 0.8362
train acc, test acc | 0.8391, 0.8377
train acc, test acc | 0.8413, 0.8406
train acc, test acc | 0.8479, 0.8487
train acc, test acc | 0.8499, 0.8484
train acc, test acc | 0.8504666666666667, 0.8474
train acc, test acc | 0.8543, 0.8521
train acc, test acc | 0.8572166666666666, 0.8545
train acc, test acc | 0.8586333333333334, 0.8565
train acc, test acc | 0.86115, 0.8579
train acc, test acc | 0.8619833333333333, 0.8581
train acc, test acc | 0.86245, 0.8605
train acc, test acc | 0.8613666666666666, 0.8588

network.py 소스의 아래 부분을 주목하자.

...
    # 가중치 매개변수의 기울기를 구한다.
    def numerical_gradient(self, x, label):
        def loss_weight(W):
            return self.loss(x, label)

        grads = {
            'W1': numerical_gradient(loss_weight, self.params['W1']),
            'b1': numerical_gradient(loss_weight, self.params['b1']),
            'W2': numerical_gradient(loss_weight, self.params['W2']),
            'b2': numerical_gradient(loss_weight, self.params['b2'])
        }

        return grads
...

run.py 소스의 호출 부분은 아래와 같다.

...
for i in range(iters_num):
    # 미니배치 획득
    batch_mask = np.random.choice(train_size, batch_size)
    batch_x = train_x[batch_mask]
    batch_labels = train_labels[batch_mask]

    # 기울기 계산
    grad = network.numerical_gradient(batch_x, batch_labels)
...

6만개의 학습데이터의 학습을 진행하면 전체 매개변수(W1, b1, W2, b2) 가 6만번 순방향으로 갱신된다.

이렇게 학습된 결과의 정확도를 그래프로 보면 아래와 같이 정확도가 86% 이상에서 안정화 되는 것을 확인할 수 있다. 위 콘솔로그에서도 확인할 수있다.

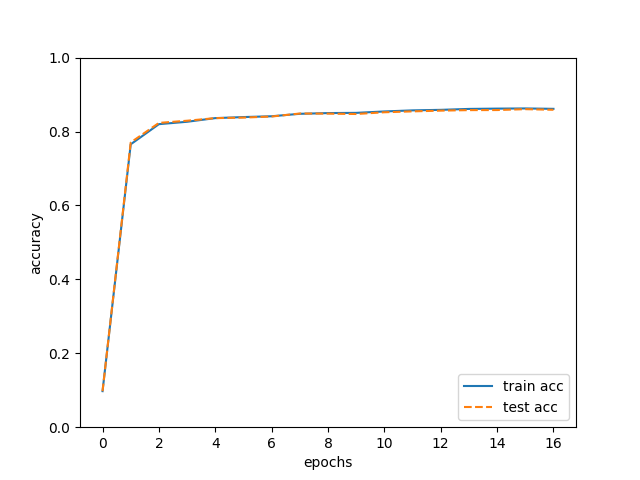
성능은 아쉽지만, 몇줄 안되는 코드로 상당히 정확한 신경망을 구성할 수 있다는 것을 확인하였다. 성능만 상당 부분 개선될 수 있다면, 데이터만 다른 것으로 바꿔 응용 분야를 넓힐 수도 있다는 것에 감이 올 것이다.

미분에서 합성함수는 합성된 개별함수의 곱으로 표현할 수 있다.

신경망에서는 마지막 출력층에서 이전 층으로 거슬러 올라가면서 미분하면 합성함수의 미분과 동일하게 코드를 구성할 수 있다.

이렇게 하면 연산량이 작아져서 상당히 빠르게 기울기를 구할 수 있다. 이 방법을 '오차역전파법' 이라고 한다.

다음 장에서는 오차역 전파법을 구현해보고, 네트워크 층을 조금더 추상화 해서 범용성을 확보해 보겠다. 더불어 속도 차이를 비교해 보겠다.

'A.I.(인공지능) & M.L.(머신러닝) > 신경망 이론' 카테고리의 다른 글

GCN 코드를 통해 이해 (0)	2024.08.14
Attention LSTM + GCN + 커머스 (0)	2024.08.13
3. 초간단 신경망(3/3) (0)	2024.02.24
1. 초 간단 신경망(1/3) (0)	2024.02.04