1. 초 간단 신경망(1/3)

신경망을 이해하기 위해서는 퍼셉트론을 이해하는 것이 좋다. 간단하게 퍼셉트론을 설명하자면 선형함수(직선의 방정식) 와 활성화 함수의 조합이라 할 수 있다. 직선의 방정식은 $y = a x + b$ 로 표현할 수 있는데, 활성화 함수는 $y$ 가 특정 임계값을 넘으면 뉴런을 활성 시키는 역할을 한다. 뉴런이 활성화 되는 것은 true, 비활성화 되는 것을 fals의 상태로 보고 논리회로를 퍼셉트론으로 구현하면서, XOR 게이트의 비선형성을 다층 퍼셉트론으로 설명한다. 단일 퍼센트론은 하나의 뉴런이고 다층 퍼셉트론은 신경망이라고 할 수 있다. 다층 퍼셉트론으로는 비선형적 경계, 다시 말해 2차원 평면상에서의 곡선, 다차원 공간에서 경계를 표현할 수 있기 때문에 신경망을 다층 퍼셉트론으로 설명한다.

여기에서는 간단한 신경망을 구현해보고, 실제 사례에 응용해 본다. 필요한 배경 이론은 최대한 간단히 설명하고 신경망의 작동 원리에 집중하겠다.

미분과 기울기

신경망의 학습은 연속된 미분으로 볼 수 있는데, 신경망 전체를 하나의 $y = f (x)$ 함수로 본다면 $y$ 결과값과 오차함수와의 차이를 줄여나가는 과정(기울기가 최소화 되는 과정) 으로 진행된다.

먼저 미분의 정의를 상기해 보자.

$f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x)}{h}$

좌표 평면에서 보면 곡선의 접선을 찾는 문제이다.

곡선 $f (x) = x^{2}$ 의 점 $P (1, 1)$ 에서의 접선

신경망의 학습 목표가 위 곡선이라면 $P (0, 0)$ 점을 찾는 문제라고 할 수 있다. 이를 파이썬 코드로 표현해 보자, 참고로 컴퓨터공학에서는 컴퓨터가 극한을 표현 할 수 없기 때문에 상당히 작은 수(통상 1/10000 이하) 를 극한값 $lim_{h \to 0}$ 으로 쓰고 미분을 할때는 중앙(중심) 차분을 수치미분을 쓴다. 중앙차분을 그림으로 표현하면 아래와 같다.

이를 수식으로 표현하면 아래와 같다.

$f^{'} (x) = lim_{h \to 0} \frac{f (x + h) - f (x - h)}{2 h}$

이를 파이썬 코드로 표현해보자.

def numerical_diff(func, x):
    # 미분의 대상은 함수이기 때문에 func 는 임의의 함수가 됨.
    
    h = 1e-4 # 1/10000
    return (func(x + h) - func(x - h)) / (2 * h)

기울기를 구해야 할 함수가 $f (x) = x^{2}$ 일때 $x = 1$ 이면 $y = 1$ 이다. 이 지점의 기울기를 구해 보자.

# 미분대상 함수
def square(x):
    return x**2;


# 수치 미분
def numerical_diff(func, x):
    h = 1e-4 # 1/10000
    return (func(x + h) - func(x - h)) / (2 * h)
    
    
# 미분을 해보자
diff = numerical_diff(square, 1)
print(diff)

미분 공식으로 보면 $x^{2}$ 의 도함수는 $2 x$ 가 되므로 $x = 1$ 일때 기울기는 $2$ 가 된다. 실제 출력값은 $1.99 . . . . . .$ 와 비슷한 근사값으로 나온다. 참고로 미분은 영어로 differentiation 이고 numerical_diff 는 수치 미분을 뜻하는 함수다.

편미분

$f (x_{0}, x_{1}) = x_{0}^{2} + x_{1}^{2}$ 수식처럼, $x$ 입력값이 여러개 있을 때의 미분을 편미분이라고 한다. 각각의 입력값을 미분 할때는 미분대상 입력값을 제외한 나머지 입력값은 상수가 된다. 구체적으로 $x_{0}$ 을 미분할 때는 $x_{1}, . . ., x_{n}$ 의 값은 상수로 처리된다. 이를 공간상의 그래프로 표현하면 다음과 같다.

$f (x_{0}, x_{1}) = x_{0}^{2} + x_{1}^{2}$ 의 그래프

위 그래프에서 특정 공간 좌표의 접선의 기울기를 구해보자, 예를 들어 $(x_{0}, x_{1}) = (3, 4)$ 의 기울기를 찾는다면 $3, 4$ 각각을 상수로 처리할 함수가 필요해진다.

# 편미분대상 임시함수, 첫번째
def partial_square_1(x0):
    return x**2 + 4**2
    

# 편미분대상 임시함수, 두번째
def partial_square_2(x1):
    return 3**2 + x1**2


# 수치 미분
def numerical_diff(func, x):
    h = 1e-4 # 1/10000
    return (func(x + h) - func(x - h)) / (2 * h)
    
    
# 미분을 해보자
diff = numerical_diff(partial_square_1, 3)
print(diff)

diff = numerical_diff(partial_square_1, 4)
print(diff)

출력은 $6.00000000000378, 7.999999999999119$ 와 비슷하게 나올 것이다.

편미분을 따로따로 계산하지 말고 한꺼번에 계산해보자. 편미분을 수식으로 표현할때는 $(\frac{\partial f}{\partial x_{0}}, \frac{\partial f}{\partial x_{1}})$ 이렇게 표현한다. 계산결과를 행렬(벡터)로 정리한 것을 기울기라고 한다. 아래 코드는 편미분 계산을 통해 기울기를 구하는 함수이다. 이제부터 행렬 계산이 필요하기 때문에 numpy 가 필요하다.

import numpy as np

# x 는 벡터(배열, 행렬) 이다
def numerical_gradient(func, x):
    h = 1e-4
    grad = np.zeros_like(x) # x와 형상이 같은 배열을 생성
    
    for idx in range(x.size):
        tmp_val = x[idx]
        # func(x + h) 게산
        x[idx] = tmp_val + h
        hp = func(x)
        
        # func(x - h) 계산
        x[idx] = tmp_val - h
        hm = func(x)
        grad[idx] = (hp - hm) / (2 * h)
        x[idx] = tmp_val # 원래 Xn 값 복원
    
    return grad

경사하강법 : 최소 기울기 찾기

경사 하강법은 기울기의 반대 방향으로 점진적으로 내려가면서 오차와의 최소 기울기를 찾는 방법이다. 수식은 아래와 같다.

$x_{0} = x_{0} - η \frac{\partial f}{\partial x_{0}}$

$x_{1} = x_{1} - η \frac{\partial f}{\partial x_{1}}$

최소 기울기를 찾는 과정을 그래프로 표현하면 아래와 같다. $- η$ 로 인해 지그재그로 내력간다. 여기서 $η$ 를 학습률(learning rate) 라고 한다.

경사하강법을 코딩으로 풀어보자

# lr : 학습률
# step_num : 학습 횟수
def gradient_descent(func, init_x, lr=0.01, step_num=100):
    x = init_x
    
    for i in range(step_num):
        grad = numerical_gradient(func, x)
        x = -lr * grad
        
    return x

활성화 함수

활성화 함수	함수식	그래프	비고
항등함수	$f (x) = x$		입력이 그대로 출력된다.
스텝함수	출력 = ${\begin{cases} 1 & w \times x + b \leq 0 \\ 0 & w \times x + b > 0 \end{cases}$		헤비사이드 스텝 함수. 이진분류 문제에 사용
시그모이드	$σ (x) = \frac{1}{1 + e^{- x}}$		전체 실수를 0과 1 구간으로 압축한다. 극단적으로 크거나 작은 값, 예외값을 제거하는 효과가 잇다. 주로 이진 분류에 사용된다.
소프트맥스	$σ (x)_{k} = \frac{e^{x_{k}}}{\sum_{i = 1}^{n} e^{x_{i}}}$		시그모이드 함수의 일반형이다. 3개 이상의 클래스를 대상으로 한 분류에 사용된다.
tanh	$t a n h (x) = \frac{e^{x} - e^{- x}}{e^{x} + e^{- x}}$		전체 실수를 -1 과 1 구간으로 압축한다. 은닉층에 사용된 tanh 함수는 대부분의 경우 시그모이드 함수보다 높은 성능을 보인다.
ReLU	출력 = ${\begin{cases} x & f (x) > 0 \\ 0 & f (x) \leq 0 \end{cases}$		입력이 0보다 클때만 발화한다. tanh 함수보다 성능이 좋아서 은닉층에 추천되는 활성화 함수이다.
Leaky ReLU	출력 = ${\begin{cases} x & f (x) > 0 \\ 0 & f (x) \times 0.01 \leq 0 \end{cases}$		x < 0 구간에서 기울기가 0이 되지 않도록 충분히 작은 값 (통상 0.01) 의 기울기를 적용

개념 설명에 많이 쓰이는 활성화 함수를 모아봤다. 소프트 맥스는 오차함수와 함께 다중 분류 작업에서 마지막 분류 확률을 계산할 때 많이 쓰이고, 은닉층의 활성화 함수로는 ReLU 함수가 많이 쓰인다.

분류 작업에 쓰일 sigmoid, softmax, relu 함수를 구현해 보자.

import numpy as np

def sigmoid(x):
    return 1 / ( 1 + np.exp(-x))
    
 
def relu(x):
    return 0 if x==0 else x
    

def softmax(x):
    max_val = np.max(x)
    exp_x = np.exp(x - max_val) # overflow 방지
    sum_exp_x = np.sum(exp_x)
    return exp_x / sum_exp_x

오차 함수

손실함수의 대표적인 함수로 평균제곱오차(mean squared error, MSE) 와 교차 엔트로피(cross entropy) 가 있다.

수식의 기호

$E (W, b)$ : 오차 함수

$W$ : 가중치 행렬

$b$ : 편향 벡터

$N$ : 학습 데이터 수

$\hat{y_{i}}$ : 출력된 예측 결과

$y_{i}$ : 실제 정답

$(\hat{y_{i}} - y_{i})$ : 일반적으로 오차 또는 잔차라고 불림.

$P$ : 확률(probability)

평균제곱오차

평균제곱오차(mean squared error, MSE)는 출력값이 실수인 회귀문제(주가 예측)에서 널리 사용하는 오참 함수이다. 단순히 레이블 값을 비교 ($ \hat{y_i) - y_i $) 하는 대신 다음 수식처럼 각 오차제곱의 평균을 구한다..

$E (W, b) = \frac{1}{N} \sum_{i = 1}^{N} (\hat{y_{i}} - y_{i})^{2}$

교차 엔트로피

교차 엔트로피(cross entropy) 는 두 확률 분포 간의 차이를 측정할 수 있다는 특성 덕분에 주로 분류 문제에서 많이 사용된다. 예를 들면 (고양이, 개, 물고기) 중에 하나로 분류하는 작업 등에 쓰일 수 있다. 수식은 아래와 같다.

$E (W, b) = - \sum_{i = 1}^{n} \sum_{j = 1}^{m} y_{i j} l o g ({\hat{y}}_{i j})$

여러개 학습 샘플 중 하나의 학습 샘플을 가지고 위 수식을 풀어보자. 가령 '개' 사진을 예측 했을 때 예측결과로 얻은 확률 분포가 다음과 같다고 하자.

$P (고 양 이) = 0.2, P (개) = 0.3, P (물 고 기) = 0.5$

실제 확률 분포와 예측 확률 분포는 얼마나 가까울까? 교차 엔트로피는 바로 이 거리를 평가할 수 있다. $y$ 가 대상 확률 분포, $p$ 가 예측 확률 분포, $m$ 이 클래스 수일 때 교차 엔트로피는 다음과 같이 정의된다.

$E (W, b) = - \sum_{i = 1}^{m} y_{i} l o g ({\hat{y}}_{i})$

확률 분포 값을 수식에 대입해 보자

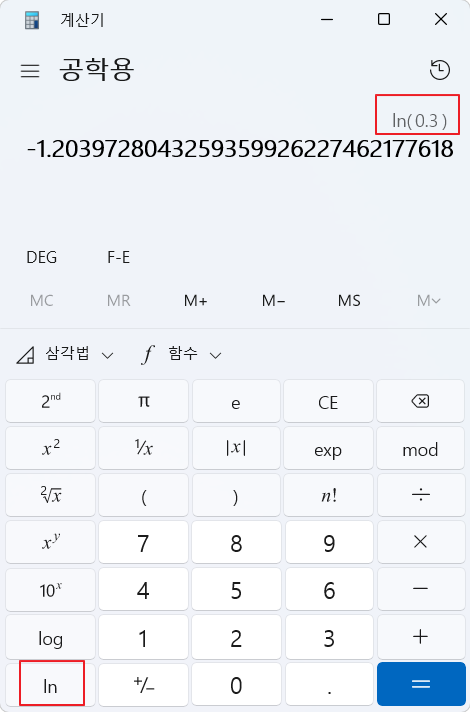
$E = - (0.0 \times l o g (0.2) + 1.0 \times l o g (0.3) + 0.0 \times l o g (0.5)) = 1.2$

실제 답인 '개' 에 더 근접하게 학습이 되 있다고 가정해 보자. 실제 답인 '개'인 확인 확율이 0.3 에서 0.5 로 높아졋다고 가정한다.

$P (고 양 이) = 0.3, P (개) = 0.5, P (물 고 기) = 0.2$

이 손실 값을 다시 계산해 보면

$E = - (0.0 \times l o g (0.3) + 1.0 \times l o g (0.5) + 0.0 \times l o g (0.2) = 0.69$

손실 값이 1.2 에서 0.69 로 줄어들었다.

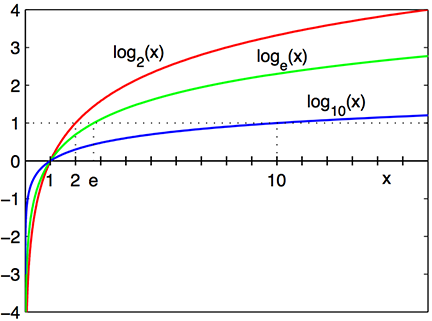
로그 함수의 기억을 되살려 보자. 밑이 2, e, 10 인 로그 함수 이다.

$l o g_{e} (X)$ 인 함수를 특별히 $l n (X)$ 함수라고 한다. 공학용 계산기를 이용해 $l n (0.3)$ 을 구해 보자 계산기 버튼에 ln 버튼이 있다.

모든 학습 샘플 $n$ 에 대해서 교차 엔트로피를 구하면 아래와 같은 식이 된다.

$E (W, b) = - \sum_{i = 1}^{n} \sum_{j = 1}^{m} y_{i j} l o g ({\hat{y}}_{i j})$

오차를 줄이려면 입력 $x$ 의 값과 답(레이블) $y$ 값은 결정되어 있으므로 가중치 파라미터 $W$ 값을 변화 시킬 수 밖에 없다. 신경망의 학습 과정은 여러개의 표본(학습 데이터셋)을 신경망에 입력해 순방향 계산을 통해 예측 결과를 계산한 다음 정답과 비교해서 오차를 계산하고 마지막으로 오차값이 최소가 될때까지 모든 노드(엣지)에 대해 가중치를 조절하는 것이다.

오차 함수를 구현해보자.

import numpy as np

def mean_squared_error(yhat, y):
    return np.sum((yhat - y) ** 2) / len(yhat)
    
    
def cross_entropy_error(yhat, y):
    delta = 1e-7 # log(0) == '무한' 회피
    return -np.sum(y + np.log(yhat + delta))

최적화 기법

배치 경사 하강법

평균제곱오차 손실함수를 다시 보자.

$E (W, b) = \frac{1}{N} \sum_{i = 1}^{N} (\hat{y_{i}} - y_{i})^{2}$

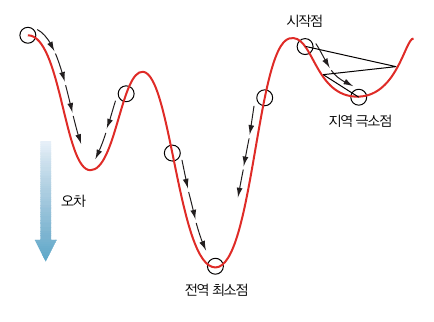
복잡한 오차함수는 여러개의 지역 최소점을 가진 경우가 있다. 우리의 목표는 전역 최소점에 도달하는 것이다.

위에서 논의한 경사하강법을 쓴다고 가정하면 처음 해야 할 일은 가중치를 초기화 하는 일이다. 가중치는 무작위한 값으로 초기화 한다. 이 때 아래 그림과 같이 지역 최소값에 갇히는 문제가 발생할 수 있다.

이 방법의 문제점은 지역 최소점에 갇히는 문제와 더불어 훈련 데이터 수 $(N)$ 가 많을 수롤 가중치를 수정하기 위해서 데이터 수만큼 손실값을 합산하기 때문에 계산 비용이 크고 속도도 느려진다. 이런 방법을 '배치 경사 하강법' 이라고 한다.

확률적 경사 하강법

확률적 경사 하강법(stochastic gradient descent, SGD)은 무작위로 데이터를 골라 가중치를 여러번 수정한다. 이 방법은 가중치에 대해 다양한 시작점을 만들 수 있으므로 여러 지역 최소점을 발견할 수 있다. 여러 지역 최소점 중 가장 작은 값을 전역 최소점으로 한다.

미니배치 경사 하강법

미니배치 경사 하강법(mini-batch gradient descent, MB-GD)은 배치 경사 하강법과 확률적 경사 하강법의 절충안이다. 경사(기울기)를 계산할 때 모든 훈련 데이터나 하나의 훈련 데이터만 사용하는 대신 훈련 데이터를 전체를 몇개의 미니 배치로 분할 다음 경사를 계산한다. BGD, SGD에 비해 계산 효율이 좋다.

2 계층 신경망

지금까지의 이론을 바탕으로 은닉층이 2계층인 신경망을 구현해 보자. 기울기와 활성화 함수를 관리 하는 소스를 일단 나누자.

gradient.py

import numpy as np


# 수치 미분
def numerical_diff(func, x):
    h = 1e-4  # 1/10000
    return (func(x + h) - func(x - h)) / (2 * h)


# x 는 벡터(배열, 행렬) 이다
def numerical_gradient(func, x):
    h = 1e-4  # 0.0001
    grad = np.zeros_like(x)

    # iterator 방식으로 행렬의 모든 원소를 순회한다.
    it = np.nditer(x, flags=['multi_index'])
    while not it.finished:
        # 행렬의 인덱스를 튜플로 제공한다.
        idx = it.multi_index
        tmp_val = x[idx]
        x[idx] = float(tmp_val) + h
        fxh1 = func(x)  # f(x+h)

        x[idx] = tmp_val - h
        fxh2 = func(x)  # f(x-h)
        grad[idx] = (fxh1 - fxh2) / (2*h)

        x[idx] = tmp_val # 값 복원
        it.iternext()

    return grad


# lr : 학습률
# step_num : 학습 횟수
def gradient_descent(func, init_x, lr=0.01, step_num=100):
    x = init_x

    for i in range(step_num):
        grad = numerical_gradient(func, x)
        x = -lr * grad

    return x

위 소스를 간단히 정리해 보면, numerical_diff 는 수치미분을 수행하는 함수이고, numerical_gradient 는 입력된 '함수'에 대해 입력값 'x' 의 기울기를 구하는 함수이다. gradietn_descent 는 학습률(lr) 의 방향(하강) 으로 반복 횟수(step_num) 만큼 수행하여 최소 기울기를 찾는 함수이다.

layers.py

import numpy as np


def sigmoid(x):
    return 1 / (1 + np.exp(-x))
    
    
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 오버플로 대책
    return np.exp(x) / np.sum(np.exp(x))


def cross_entropy_error(y, label):
    if y.ndim == 1:
        label = label.reshape(1, label.size)
        y = y.reshape(1, y.size)

    # 훈련데이터의 레이블이 one-hot 벡터일때([0, 0, 0, 0, 0, 0, 1, 0, 0, 0] => 6)는 인덱스로 변환
    if label.size == y.size:
        label = label.argmax(axis=1)

    batch_size = y.shape[0]
    delta = 1e-7  # log(0) == '무한' 회피

    # 각 정답 레이블에 해당하는 데이터의 예측 확률값(y[np.arange(batch_size), label]) 의 오차값을 반환
    return -np.sum(label * np.log(y[np.arange(batch_size), label] + delta)) / batch_size

소프트맥스 함수에서 데이터의 형태가 2차원 배열일때 각 로우의 최대값을 뽑기위해 전치행렬을 이용하는 방법으로 한꺼번에 소프트맥스 값을 계산한다. gradient.py, layers.py 두개 소스를 이용해서 딥러닝의 'Hello world' 격인 'Mnist' 손글씨 데이터 셋으로 숫자 맞추기를 구현해 보자.

'A.I.(인공지능) & M.L.(머신러닝) > 신경망 이론' 카테고리의 다른 글

GCN 코드를 통해 이해 (0)	2024.08.14
Attention LSTM + GCN + 커머스 (1)	2024.08.13
3. 초간단 신경망(3/3) (0)	2024.02.24
2. 초간단 신경망(2/3) (0)	2024.02.17